Introducción
En esta publicación se mostrará al lector cómo simular datos de un modelo lineal (sin y con efectos aleatorios) y la forma de estimar los parámetros. Los modelos a considerar son:
- Modelo lineal clásico,
- Modelo lineal con intercepto aleatorio,
- Modelo lineal con pendiente aleatoria,
- Modelo lineal con intercepto y pendiente aleatoria.
Ilustración de un modelo mixto
Se recomienda al lector que visite este enlace para que vea una ilustración muy interesante de modelos mixtos. Los parámetros usados en las simulaciones aquí realizadas fueron inspirados en la ilustración.
Simulando datos de modelo lineal clásico
Suponga que queremos simular n=50 observaciones del siguiente modelo con vector de parámetros \boldsymbol{\Theta}=(\beta_0=59, \beta_1=1, \sigma=1)^\top. El modelo de interés es el siguiente.
\begin{align*} y_i &\sim \mathcal{N}(\mu_i, \sigma^2) \\ \mu_i &= 59 + 1 \, x_i \\ \sigma &= 1 \\ x &\sim Uniforme[1, 9] \end{align*}
Con el siguiente código se simula el conjunto de datos de interés.
n <- 50
x <- sample(1:9, size=n, replace=TRUE) # Uniforme discreta [1, 9]
sig <- 1
media <- 59 + 1 * x
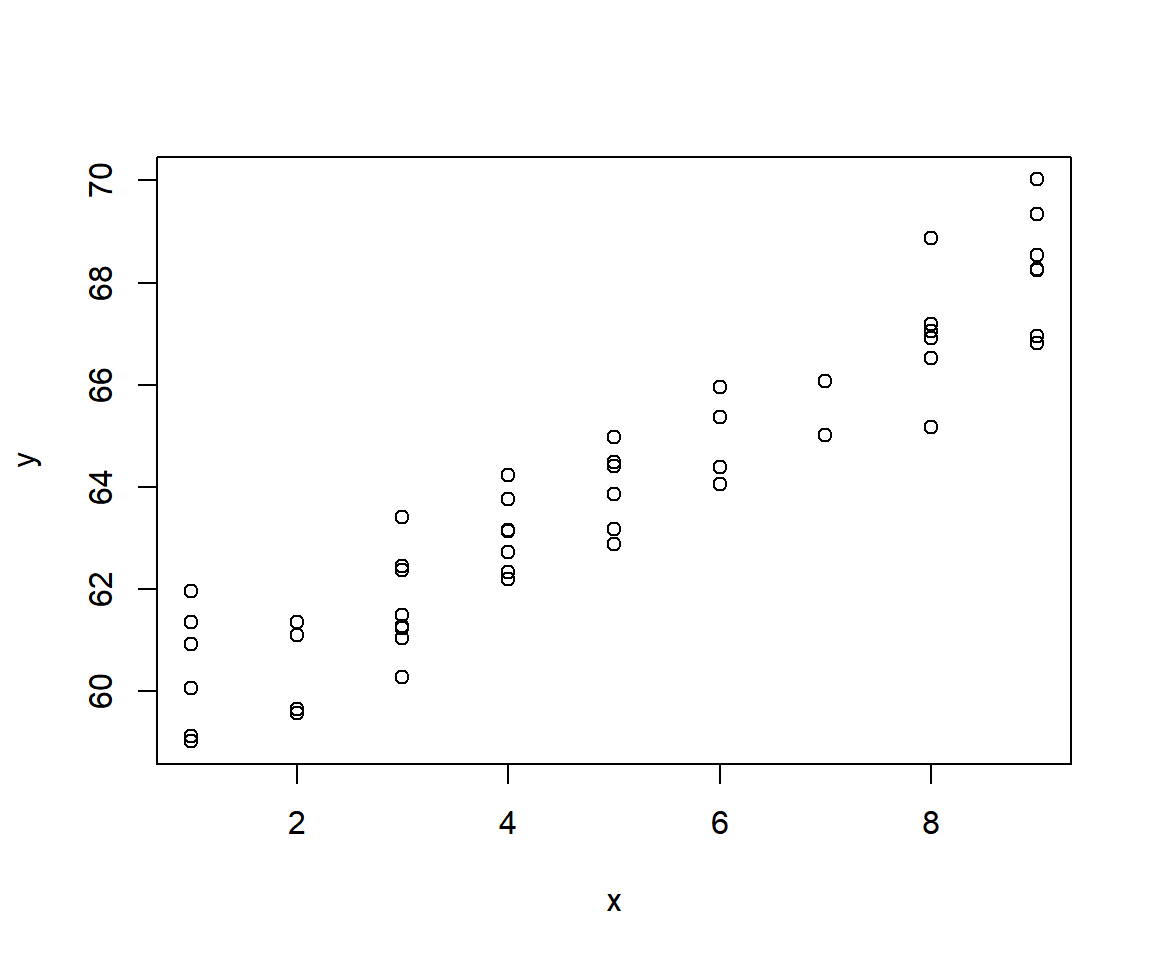
y <- rnorm(n=n, mean=media, sd=sig)Vamos a construir un diagrama de dispersión para los datos simulados.
plot(y ~ x)Ajustemos un modelo para recuperar el vector de parámetros parámetros \boldsymbol{\Theta}.
mod1 <- lm(y ~ x)
c(mod1$coef, sigma=summary(mod1)$sigma)## (Intercept) x sigma
## 58.8748633 1.0208996 0.9725214De la salida anterior vemos que vector de parámetros estimado está cerca de \boldsymbol{\Theta}=(\beta_0=59, \beta_1=1, \sigma=1)^\top.
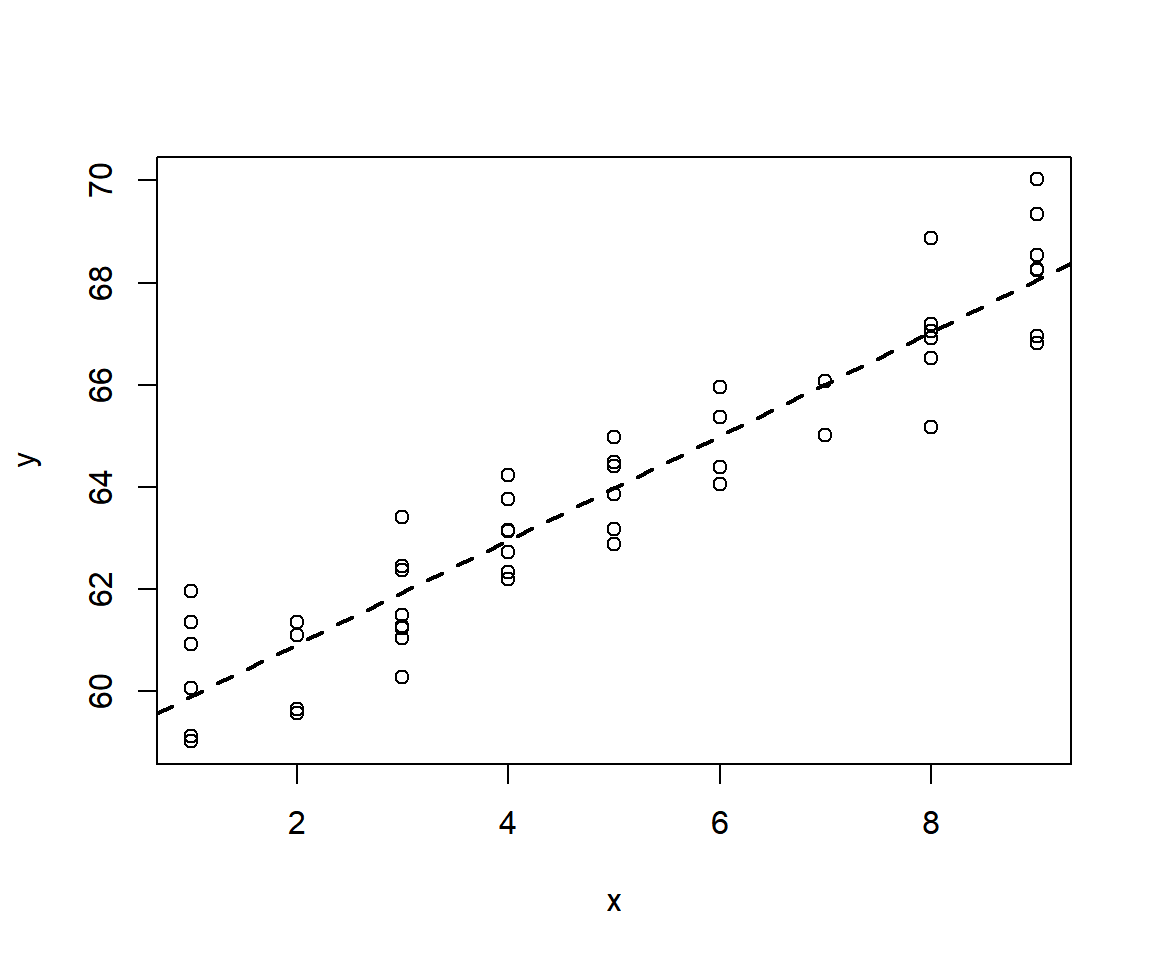
Vamos a agregar la línea del modelo ajustado.
plot(y ~ x)
abline(mod1, lty='dashed', lwd=2)Simulando datos con intercepto aleatorio
Suponga que ahora queremos simular n_i=10 observaciones para n_g=5 grupos (en total 50) usando el siguiente modelo mixto con intercepto aleatorio con vector de parámetros \boldsymbol{\Theta}=(\beta_0=59, \beta_1=1, \sigma=1, \sigma_{b0}=10)^\top. El modelo de interés es el siguiente.
\begin{align*} y_{ij} &\sim \mathcal{N}(\mu_{ij}, \sigma^2) \\ \mu_{ij} &= 59 + 1 \, x_{ij} + b_{0i} \\ \sigma &= 1 \\ b_0 &\sim \mathcal{N}(0, \sigma_{b0}^2) \\ x &\sim Uniforme[1, 9] \\ i &= 1, 2, \ldots, n_g \quad j=1, 2, \ldots, n_i \end{align*}
sig <- 1
sd_b0 <- 10
ng <- 5 # número de grupos
ni <- 10 # número de obs por grupo
n <- ng * ni # número de obs total
grupo <- rep(1:5, each=ni) # Variable de agrupación
x <- sample(1:9, size=n, replace=TRUE)
b0 <- rnorm(n=ng, mean=0, sd=sd_b0) # Vector con los cinco b0
b0_rep <- rep(b0, each=ni) # Vector con los b0 repetidos
media <- 59 + 1 * x + b0_rep
y <- rnorm(n=n, mean=media, sd=sig)
dt <- data.frame(grupo=grupo, x=x, b0_rep, y=y)Exploremos lo que hay dentro de dt.
dt[1:15, ]## grupo x b0_rep y
## 1 1 4 8.507035 70.57511
## 2 1 8 8.507035 76.45732
## 3 1 9 8.507035 77.86659
## 4 1 1 8.507035 70.29329
## 5 1 8 8.507035 74.71067
## 6 1 7 8.507035 74.85484
## 7 1 2 8.507035 69.60829
## 8 1 5 8.507035 71.18486
## 9 1 6 8.507035 72.12007
## 10 1 8 8.507035 75.78424
## 11 2 3 11.603689 71.82179
## 12 2 6 11.603689 75.97606
## 13 2 8 11.603689 78.63925
## 14 2 9 11.603689 79.55625
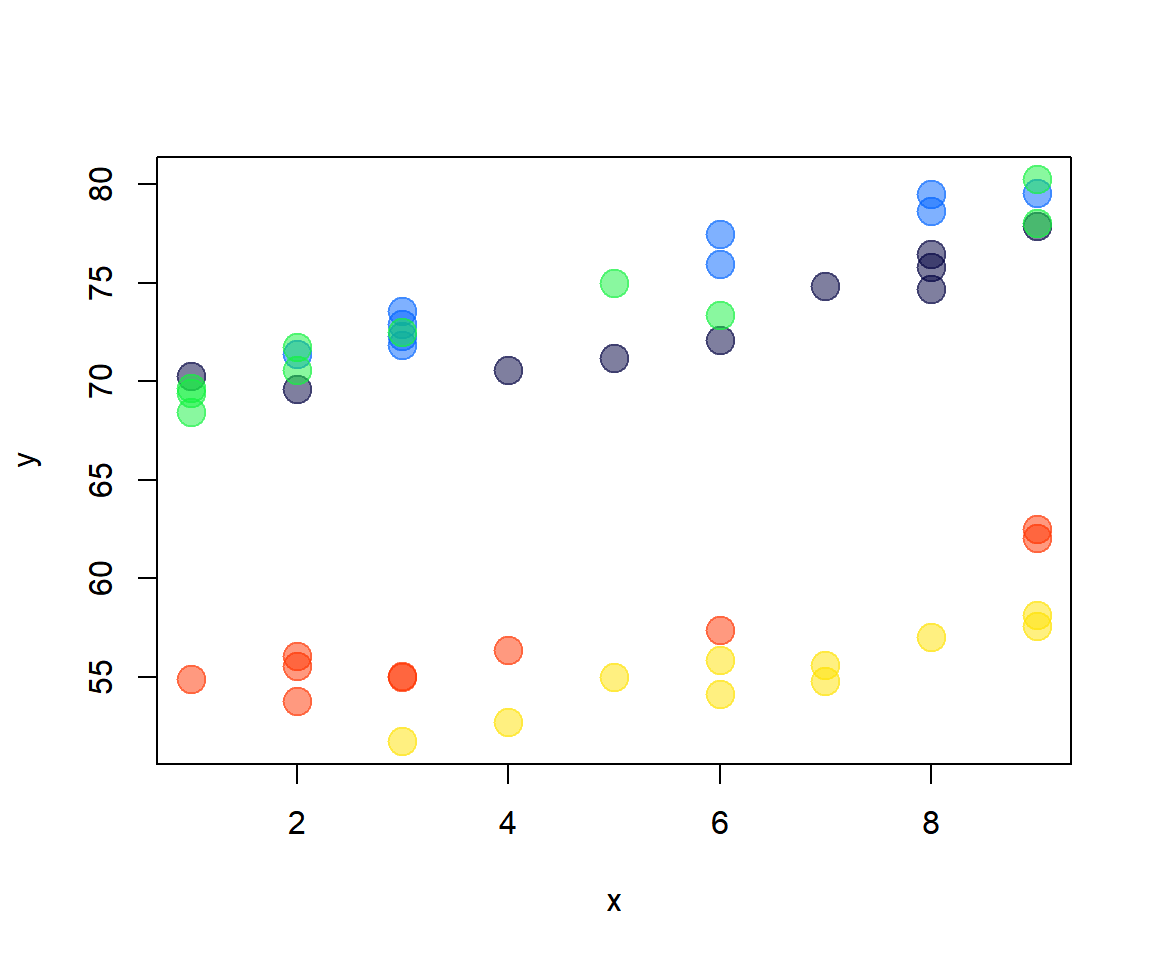
## 15 2 3 11.603689 72.92343Vamos a construir un diagrama de dispersión para los datos simulados.
colores <- c("#00004080", "#0063FF80", "#13F24080", "#FFE20180", "#FF330080")
with(dt, plot(y ~ x, pch=20, col=colores[dt$grupo], cex=3))Ajustemos un modelo para recuperar el vector de parámetros parámetros \boldsymbol{\Theta}, para esto usemos la función lme del paquete nlme.
library(nlme)
mod2 <- lme(y ~ x, random = ~ 1 | grupo, data=dt)
summary(mod2)## Linear mixed-effects model fit by REML
## Data: dt
## AIC BIC logLik
## 179.4033 186.8881 -85.70164
##
## Random effects:
## Formula: ~1 | grupo
## (Intercept) Residual
## StdDev: 10.07783 0.9749663
##
## Fixed effects: y ~ x
## Value Std.Error DF t-value p-value
## (Intercept) 61.28547 4.517156 44 13.56727 0
## x 1.07718 0.053448 44 20.15361 0
## Correlation:
## (Intr)
## x -0.06
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -1.85108147 -0.69513052 -0.02213694 0.73103696 2.17818479
##
## Number of Observations: 50
## Number of Groups: 5De la tabla anterior vemos que el vector de parámetros estimado \hat{\boldsymbol{\Theta}} no está tan alejado de \boldsymbol{\Theta}.
Los efectos fijos estimados \beta_0 y \beta_1 se obtienen así:
fixef(mod2)## (Intercept) x
## 61.285466 1.077179Vamos a recuperar las predicciones de los 5 interceptos aleatorios \tilde{b}_{0} (efectos aleatorios) y a compararlas con los verdaderos b_{0}.
cbind(ranef(mod2), b0)## (Intercept) b0
## 1 5.806989 8.507035
## 2 8.529134 11.603689
## 3 7.403059 10.031706
## 4 -12.905423 -10.733982
## 5 -8.833760 -6.713931De la tabla anterior vemos que los \tilde{b_{0}} son cercanos a los verdaderos b_{0} simulados.
Usando los efectos fijos y los efectos aleatorios podemos obtener las expresiones (\hat{\beta}_0 + \hat{\beta}_1 x_{ij} + \tilde{b}_{0i}) para los modelos de cada grupo así:
coef(mod2)## (Intercept) x
## 1 67.09246 1.077179
## 2 69.81460 1.077179
## 3 68.68852 1.077179
## 4 48.38004 1.077179
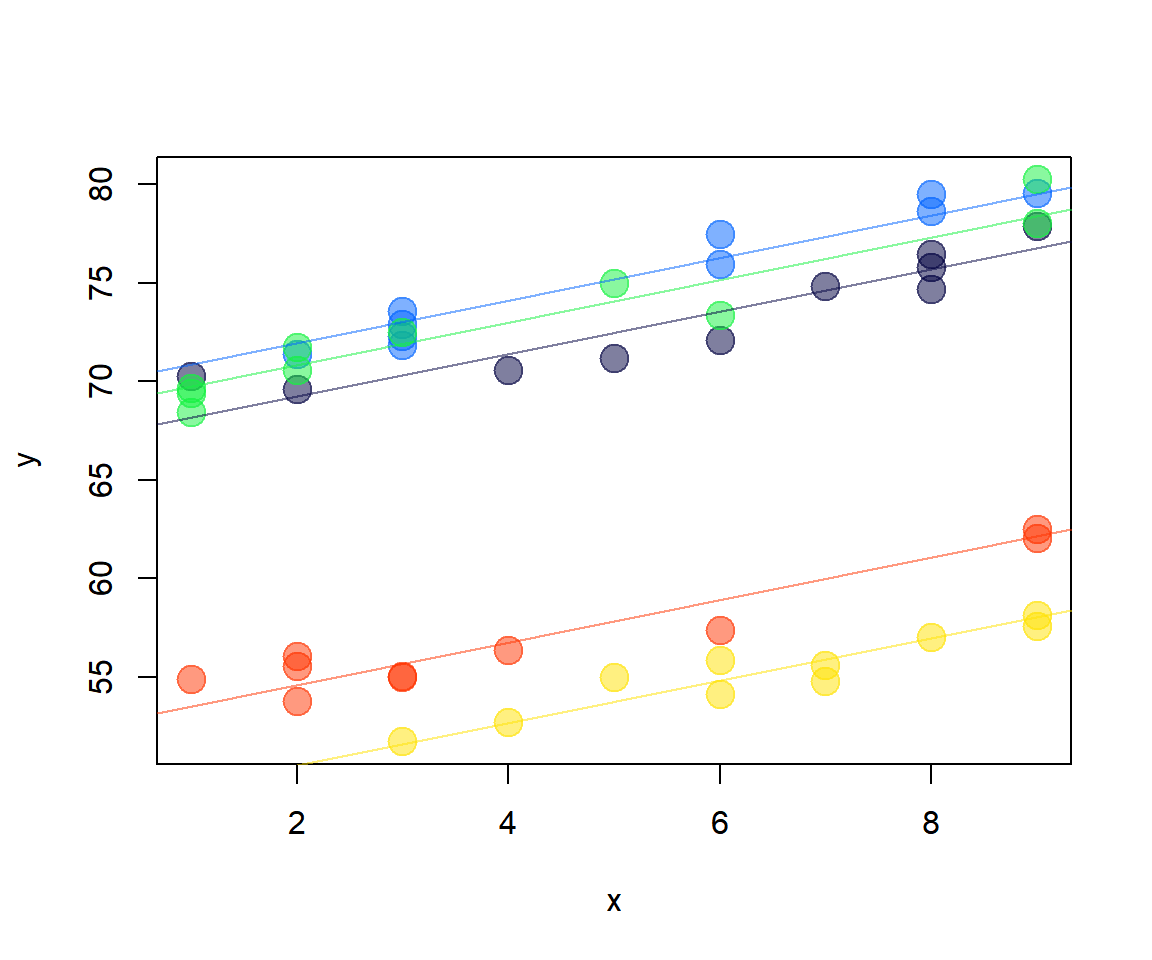
## 5 52.45171 1.077179Usando la información anterior se puede dibujar el modelo ajustado para cada grupo.
coef <- coef(mod2)
with(dt, plot(y ~ x, pch=20, col=colores[dt$grupo], cex=3))
for (i in 1:5) abline(a=coef[i, 1], b=coef[i, 2], col=colores[i])Simulando datos con pendiente aleatoria
Suponga que ahora queremos simular n_i=10 observaciones para n_g=5 grupos (en total 50) usando el siguiente modelo mixto con pendiente aleatoria con vector de parámetros \boldsymbol{\Theta}=(\beta_0=59, \beta_1=1, \sigma=1, \sigma_{b1}=5)^\top. El modelo de interés es el siguiente.
\begin{align*} y_{ij} &\sim \mathcal{N}(\mu_{ij}, \sigma^2) \\ \mu_{ij} &= 59 + 1 \, x_{ij} + b_{1i} \, x_{ij} \\ \sigma &= 1 \\ b_1 &\sim \mathcal{N}(0, \sigma_{b1}^2) \\ x &\sim Uniforme[1, 9] \\ i &= 1, 2, \ldots, n_g, \quad j=1, 2, \ldots, n_i \end{align*}
sig <- 1
sd_b1 <- 5
ng <- 5
ni <- 10
n <- ng * ni
grupo <- rep(1:5, each=ni)
n <- ng * ni
x <- sample(1:9, size=n, replace=TRUE)
b1 <- rnorm(n=ng, mean=0, sd=sd_b0)
b1_rep <- rep(b0, each=ni)
media <- 59 + 1 * x + b1_rep * x
y <- rnorm(n=n, mean=media, sd=sig)
dt <- data.frame(grupo=grupo, x=x, b1_rep, y=y)Exploremos lo que hay dentro de dt.
dt[1:15, ]## grupo x b1_rep y
## 1 1 9 8.507035 143.89291
## 2 1 9 8.507035 144.23680
## 3 1 5 8.507035 106.93728
## 4 1 3 8.507035 87.86692
## 5 1 6 8.507035 116.47136
## 6 1 7 8.507035 125.46592
## 7 1 3 8.507035 86.47815
## 8 1 2 8.507035 77.80319
## 9 1 3 8.507035 88.09359
## 10 1 9 8.507035 146.06308
## 11 2 8 11.603689 160.22958
## 12 2 7 11.603689 146.80129
## 13 2 7 11.603689 148.09777
## 14 2 4 11.603689 109.07502
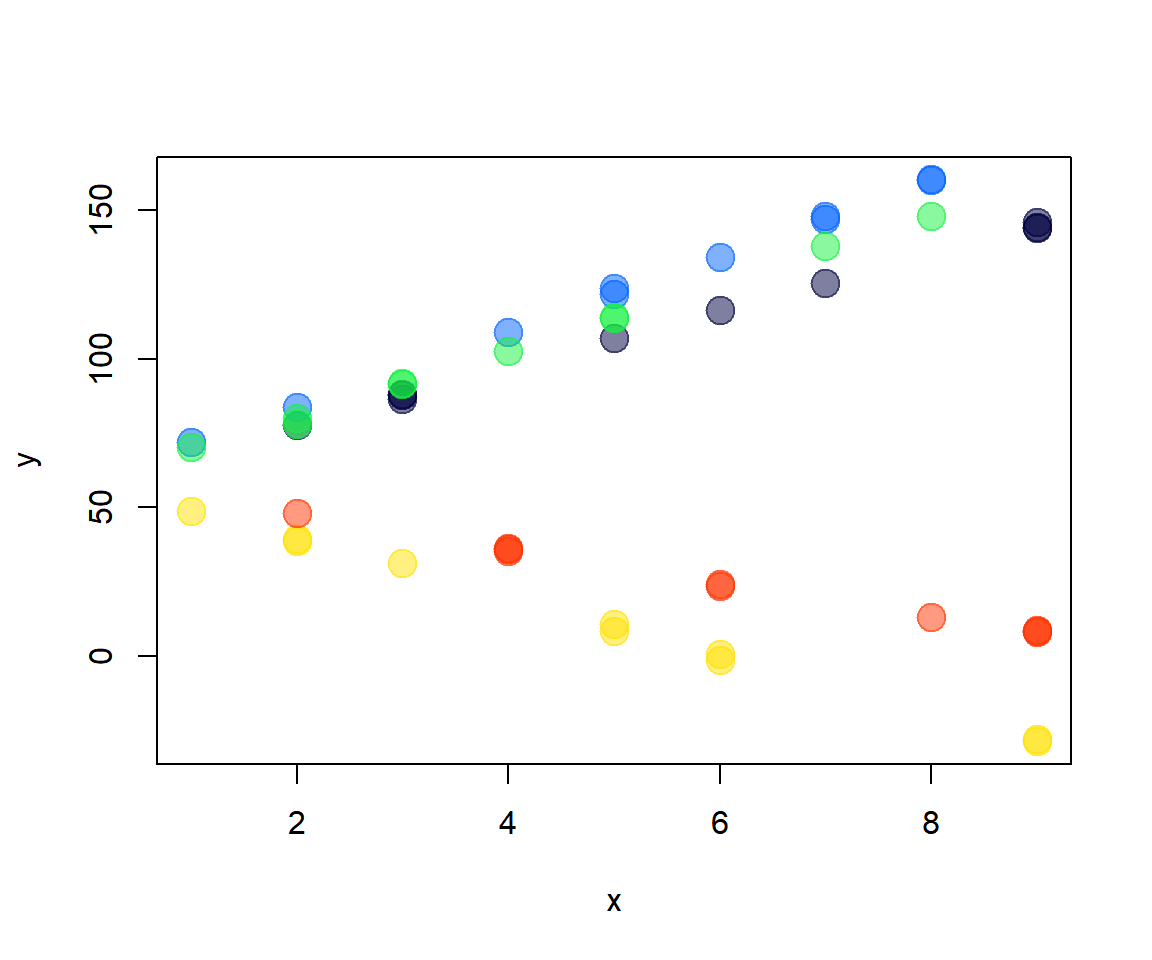
## 15 2 1 11.603689 71.91539Vamos a construir un diagrama de dispersión para los datos simulados.
with(dt, plot(y ~ x, pch=20, col=colores[dt$grupo], cex=3))Ajustemos un modelo para recuperar el vector de parámetros parámetros \boldsymbol{\Theta}, para esto usemos la función lme del paquete nlme.
mod3 <- lme(y ~ x, random = ~ -1 + x | grupo, data=dt)
summary(mod3)## Linear mixed-effects model fit by REML
## Data: dt
## AIC BIC logLik
## 185.8112 193.296 -88.90559
##
## Random effects:
## Formula: ~-1 + x | grupo
## x Residual
## StdDev: 10.45577 0.8936561
##
## Fixed effects: y ~ x
## Value Std.Error DF t-value p-value
## (Intercept) 58.36815 0.291970 44 199.91138 0.000
## x 3.65236 4.676252 44 0.78104 0.439
## Correlation:
## (Intr)
## x -0.01
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -2.91868086 -0.52963861 0.05796967 0.62106869 2.02802833
##
## Number of Observations: 50
## Number of Groups: 5Los efectos fijos estimados \beta_0 y \beta_1 se obtienen así:
fixef(mod3)## (Intercept) x
## 58.368150 3.652363Vamos a recuperar las predicciones de las 5 pendientes aleatorios (efectos aleatorios) y a compararlas con los verdaderos b_{1}.
cbind(ranef(mod3), b1)## x b1
## 1 5.966839 9.549974
## 2 9.086261 3.488025
## 3 7.506486 -11.447336
## 4 -13.317471 1.427556
## 5 -9.242115 8.070870Usando los efectos fijos y los efectos aleatorios podemos obtener las expresiones (\hat{\beta}_0 + \hat{\beta}_1 x_{ij} + b_{1i} x_{ij}) para los modelos de cada grupo así:
coef(mod3)## (Intercept) x
## 1 58.36815 9.619202
## 2 58.36815 12.738623
## 3 58.36815 11.158848
## 4 58.36815 -9.665108
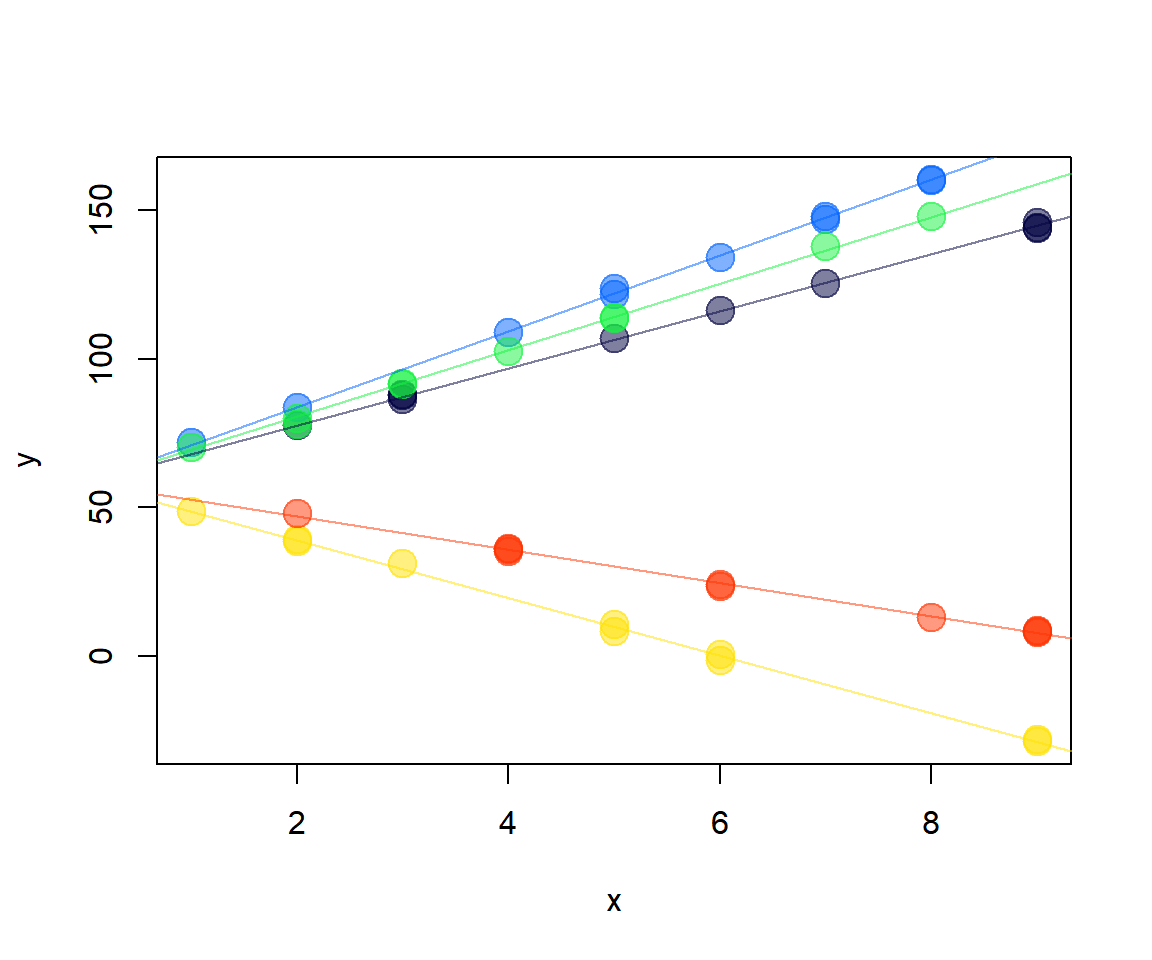
## 5 58.36815 -5.589752Usando la información anterior se puede dibujar el modelo ajustado para cada grupo.
coef <- coef(mod3)
with(dt, plot(y ~ x, pch=20, col=colores[dt$grupo], cex=3))
for (i in 1:5) abline(a=coef[i, 1], b=coef[i, 2], col=colores[i])Simulando datos con intercepto y pendiente aleatoria
Suponga que ahora queremos simular n_i=10 observaciones para n_g=5 grupos (en total 50) usando el siguiente modelo mixto con intercepto y pendiente aleatoria con vector de parámetros \boldsymbol{\Theta}=(\beta_0=59, \beta_1=1, \sigma=1, \sigma_{b0}=9, \sigma_{b0}=4, \sigma_{b01}=-2)^\top.
\begin{equation} \begin{split} y_{ij} &\sim \mathcal{N}(\mu_{ij}, \sigma^2), \\ \mu_{ij} &= 59 + 1 \, x_{ij} + b_{0i} + b_{1i} \, x_{ij} \\ \left ( \begin{matrix} b_{0i} \\ b_{1i} \end{matrix} \right ) &\sim \mathcal{N}\left ( \left ( \begin{matrix} 0 \\ 0 \end{matrix} \right ), \left ( \begin{matrix} \sigma^2_{b0} & \sigma_{b01} \\ \sigma_{b01} & \sigma^2_{b1} \end{matrix} \right ) \right ) \\ x &\sim Uniforme[1, 9] \\ i &= 1, 2, \ldots, n_g \quad j=1, 2, \ldots, n_i \end{split} \end{equation}
ng <- 5
ni <- 10
n <- ng * ni
sig <- 1
sd_b0 <- 9 # Matriz de covarianzas de los efectos aleatorios
sd_b1 <- 4
sd_b0b1 <- -2
library(MASS)
mu <- c(0, 0)
Sigma <- matrix(c(sd_b0^2, sd_b0b1, sd_b0b1, sd_b1^2), ncol=2)
b <- mvrnorm(n=ng, mu=mu, Sigma=Sigma)
b_rep <- b[rep(1:nrow(b), each=ni), ]
grupo <- rep(1:5, each=ni)
x <- sample(1:9, size=n, replace=TRUE)
media <- 59 + 1 * x + b_rep[, 1] + b_rep[, 2] * x
y <- rnorm(n=n, mean=media, sd=sig)
dt <- data.frame(grupo=grupo, x=x, b0=b_rep[, 1], b1=b_rep[, 2], y=y)Exploremos lo que hay dentro de dt.
dt[1:15, ]## grupo x b0 b1 y
## 1 1 3 4.4592886 8.497444 91.50567
## 2 1 9 4.4592886 8.497444 149.44340
## 3 1 1 4.4592886 8.497444 74.21884
## 4 1 2 4.4592886 8.497444 81.98274
## 5 1 8 4.4592886 8.497444 140.22555
## 6 1 7 4.4592886 8.497444 130.63046
## 7 1 8 4.4592886 8.497444 139.84987
## 8 1 8 4.4592886 8.497444 138.33806
## 9 1 6 4.4592886 8.497444 120.50308
## 10 1 8 4.4592886 8.497444 139.85333
## 11 2 2 0.4179834 -1.132215 58.44290
## 12 2 3 0.4179834 -1.132215 58.26912
## 13 2 5 0.4179834 -1.132215 58.22999
## 14 2 7 0.4179834 -1.132215 58.34172
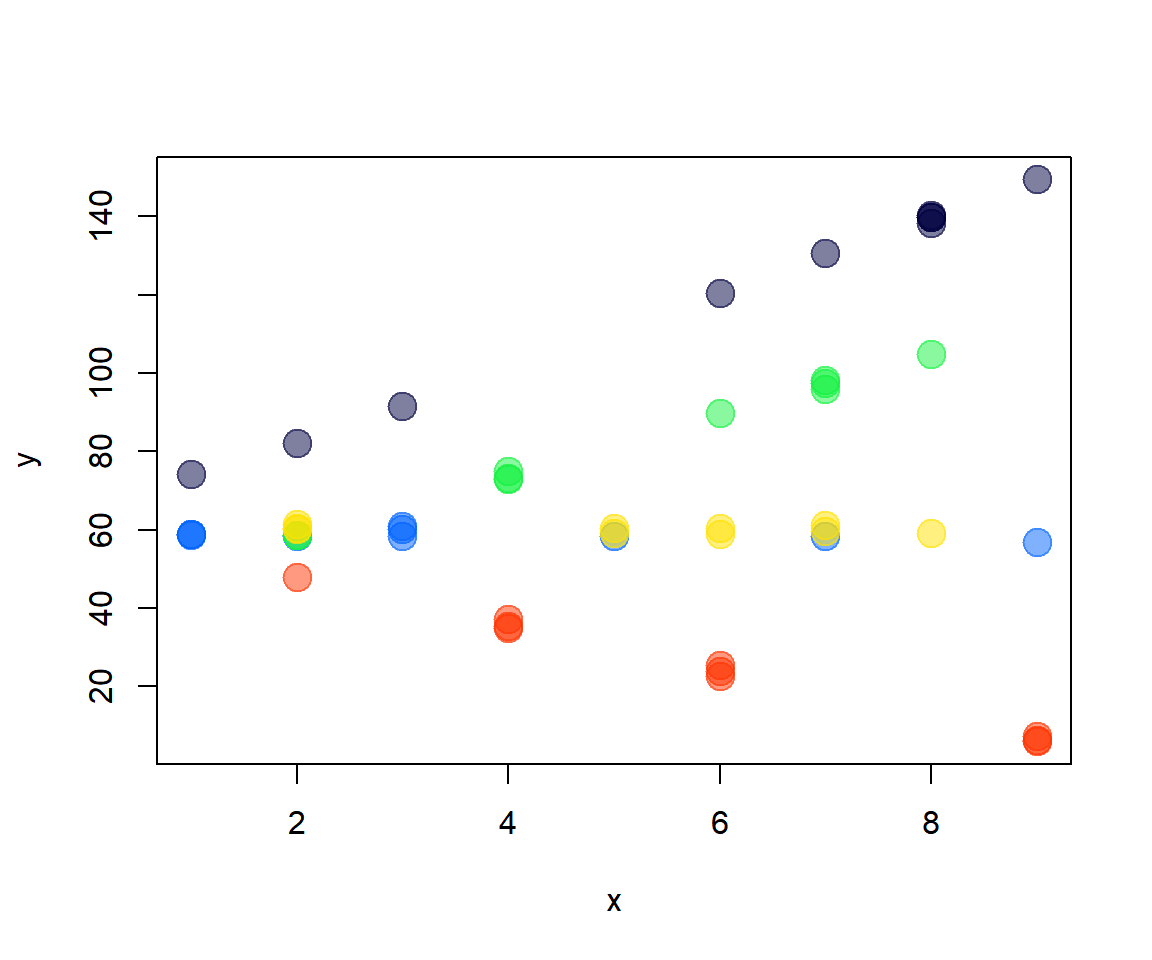
## 15 2 1 0.4179834 -1.132215 58.81600Vamos a construir un diagrama de dispersión para los datos simulados.
with(dt, plot(y ~ x, pch=20, col=colores[dt$grupo], cex=3))Ajustemos un modelo para recuperar el vector de parámetros parámetros \boldsymbol{\Theta}, para esto usemos la función lme del paquete nlme.
mod4 <- lme(y ~ x, random = ~ 1 + x | grupo, data=dt)
summary(mod4)## Linear mixed-effects model fit by REML
## Data: dt
## AIC BIC logLik
## 205.9604 217.1876 -96.98019
##
## Random effects:
## Formula: ~1 + x | grupo
## Structure: General positive-definite, Log-Cholesky parametrization
## StdDev Corr
## (Intercept) 8.1128287 (Intr)
## x 6.3385798 -0.306
## Residual 0.9018211
##
## Fixed effects: y ~ x
## Value Std.Error DF t-value p-value
## (Intercept) 57.30134 3.641324 44 15.736402 0.000
## x 2.18995 2.835224 44 0.772409 0.444
## Correlation:
## (Intr)
## x -0.307
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -1.7654779 -0.6758214 -0.1068154 0.5118184 2.3337490
##
## Number of Observations: 50
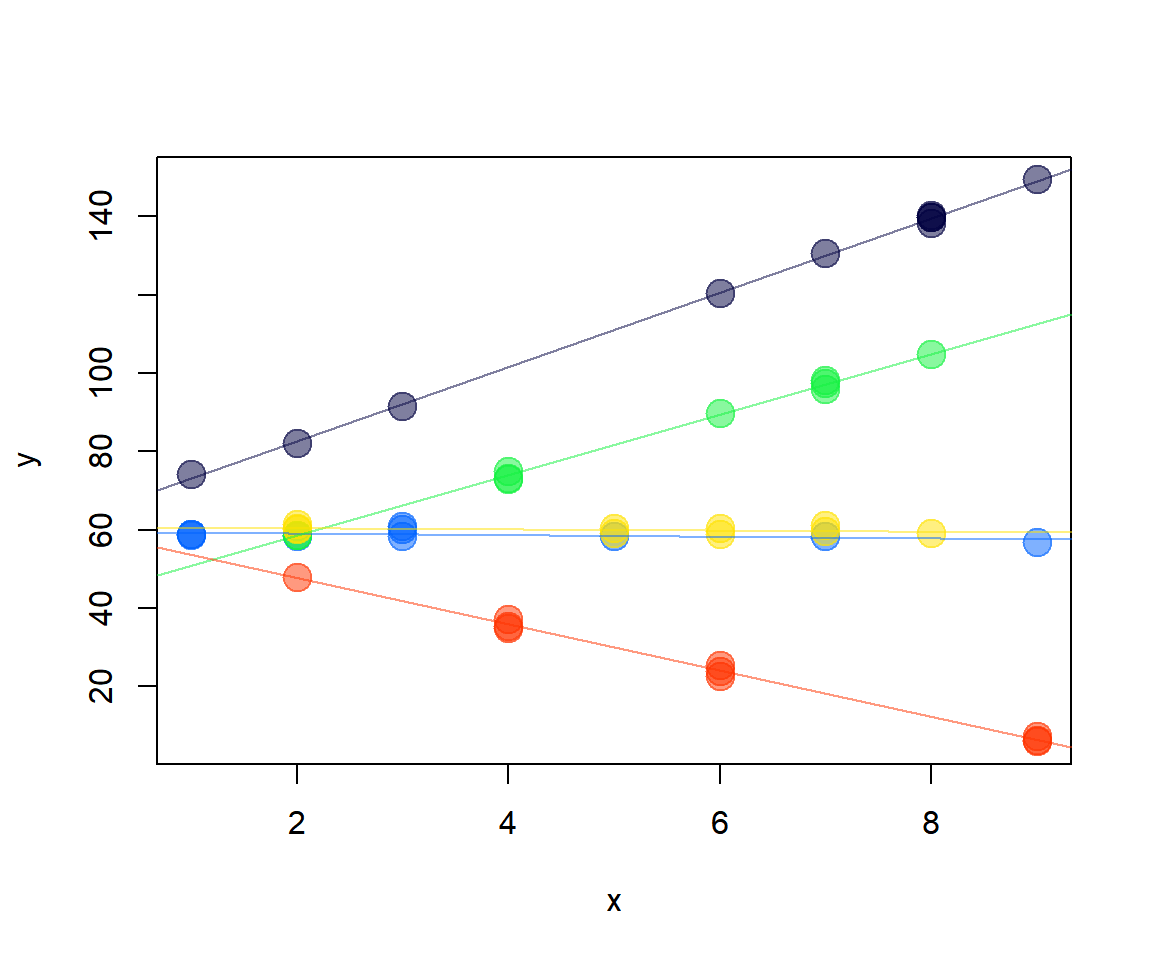
## Number of Groups: 5Al igual que en los ejemplos anteriores, se puede dibujar el modelo ajustado para cada grupo.
coef <- coef(mod4)
with(dt, plot(y ~ x, pch=20, col=colores[dt$grupo], cex=3))
for (i in 1:5) abline(a=coef[i, 1], b=coef[i, 2], col=colores[i])Tarea
- ¿Es posible que en un modelo mixto y se distribuya no normal?
- Consultar en la web ejemplos sencillos (con una sola covariable x) de modelos mixtos en los cuales la variable respuesta siga una distribución Poisson, binomial y gamma.
- Para cada uno de los ejemplos encontrados, simular datos usando la estructura del ejemplo y luego estimar los parámetros.