Redes neuronales con neuralnet

Introducción

En esta publicación se mostrará como usar redes neuronales para predecir el valor de una variable $Y$ en función de una sola covariable $X$ usando redes neuronales por medio del paquete neuralnet.

Los datos

En esta publicación vamos a usar los datos del ejemplo 2.1 del libro de Montgomery, Peck and Vining (2003). En el ejemplo 2.1 los autores ajustaron un modelo de regresión lineal simple para explicar la Resistencia ( $Y$ ) de una soldadura en función de la Edad ( $X$ ) de la misma. A continuación una figura ilustrativa del problema.

Figura: Ilustración del problema

A continuación el código para cargar los datos y una muestra de las 6 primeras observaciones de la base de datos, en total tenemos 20 observaciones.

file <- "https://raw.githubusercontent.com/fhernanb/datos/master/propelente"
datos <- read.table(file=file, header=TRUE)
head(datos) # shows the first 6 rows

##   Resistencia  Edad
## 1     2158.70 15.50
## 2     1678.15 23.75
## 3     2316.00  8.00
## 4     2061.30 17.00
## 5     2207.50  5.50
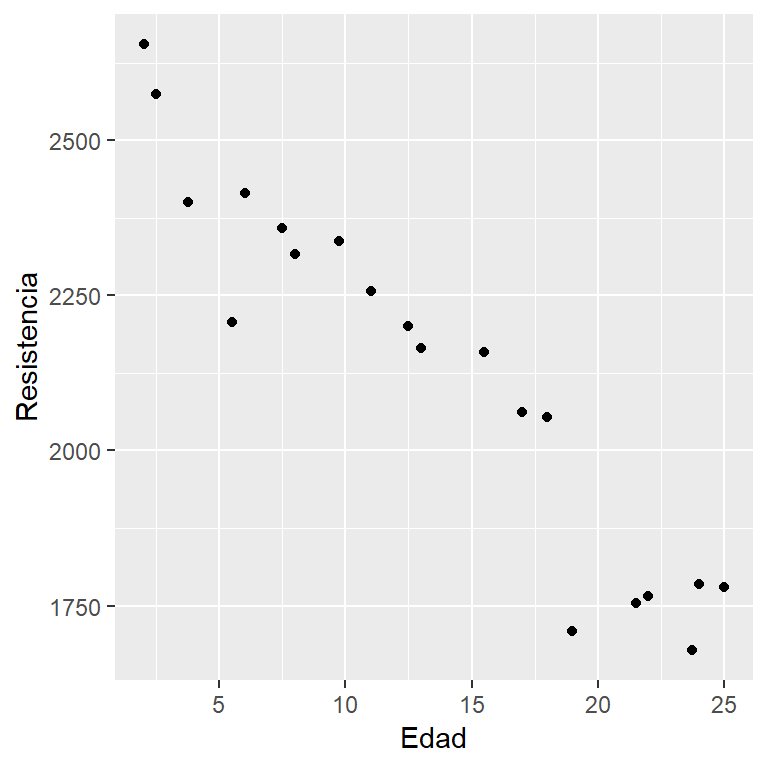
## 6     1708.30 19.00

Para crear un diagrama de dispersión que nos muestre la relación entre las dos variables usamos las siguientes instrucciones.

library(ggplot2)
ggplot(datos, aes(x=Edad, y=Resistencia)) + geom_point()

Paquete `neuralnet`

En este ejemplo vamos a usar la función neuralnet del paquete neuralnet para crear la red neuronal. La función neuralnet tiene la siguiente estructura.

neuralnet(formula, data, hidden = 1, threshold = 0.01,
  stepmax = 1e+05, rep = 1, startweights = NULL,
  learningrate.limit = NULL, learningrate.factor = list(minus = 0.5,
  plus = 1.2), learningrate = NULL, lifesign = "none",
  lifesign.step = 1000, algorithm = "rprop+", err.fct = "sse",
  act.fct = "logistic", linear.output = TRUE, exclude = NULL,
  constant.weights = NULL, likelihood = FALSE)

Para conocer en detalle la función se recomienda al lector escribir en la consola de R help(neuralnet).

Creando la red neuronal

Antes de crear la red es necesario escalar las variables para evitar el efecto de la escala de las variables. Existen varias formas de escalar pero aquí vamos a usar una transformación para pasar los valores de las variables al intervalo $(0, 1)$ .

Con el siguiente código vamos a convertir los datos originales del objeto datos a los datos escalados y se almacenarán en el objeto scaled.

maxs <- apply(datos, 2, max) 
mins <- apply(datos, 2, min)
scaled <- as.data.frame(scale(datos, center=mins, scale=maxs-mins))

A continuación vamos a comparar las primeras 6 filas de datos y de scaled para ver lo que sucedió.

head(cbind(datos, scaled))

##   Resistencia  Edad Resistencia      Edad
## 1     2158.70 15.50  0.49234158 0.5869565
## 2     1678.15 23.75  0.00000000 0.9456522
## 3     2316.00  8.00  0.65350136 0.2608696
## 4     2061.30 17.00  0.39255161 0.6521739
## 5     2207.50  5.50  0.54233902 0.1521739
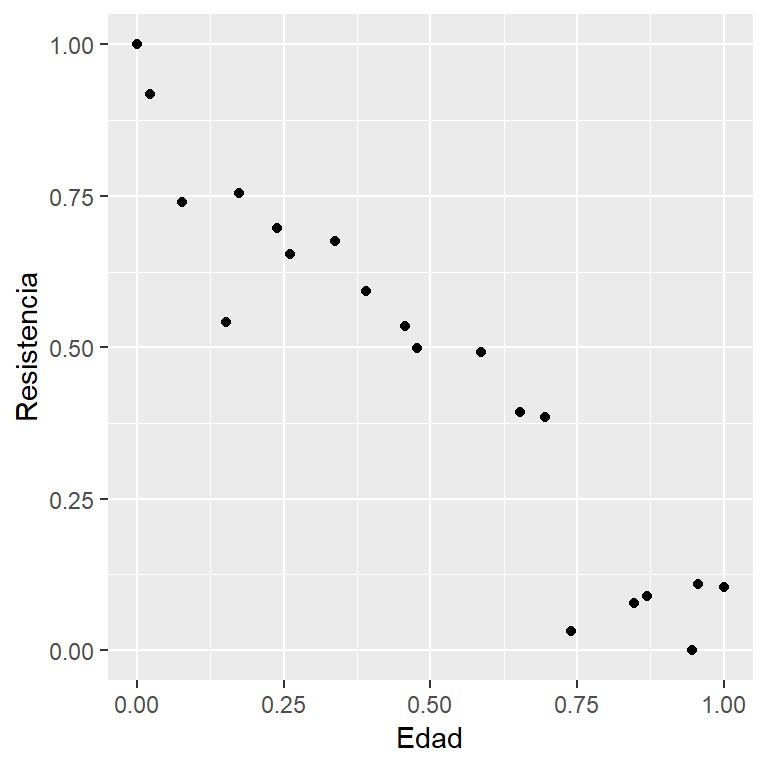
## 6     1708.30 19.00  0.03088981 0.7391304

En la siguiente figura se muestra el diagrama de dispersión para las variables escaladas. Al comparar ambos gráficos de dispersión (con datos y con scaled) se observa el mismo patrón en la nube de puntos, la única diferencia es que ahora los valores de las variables ( $Y$ y $X$ ) están en $(0, 1)$ .

ggplot(scaled, aes(x=Edad, y=Resistencia)) + geom_point()

La primera red neuronal a considerar se llamará mod1 y tendrá una capa con un solo nodo. El código para crear la red es el siguiente.

library(neuralnet)
mod1 <- neuralnet(Resistencia ~ Edad, data=scaled, 
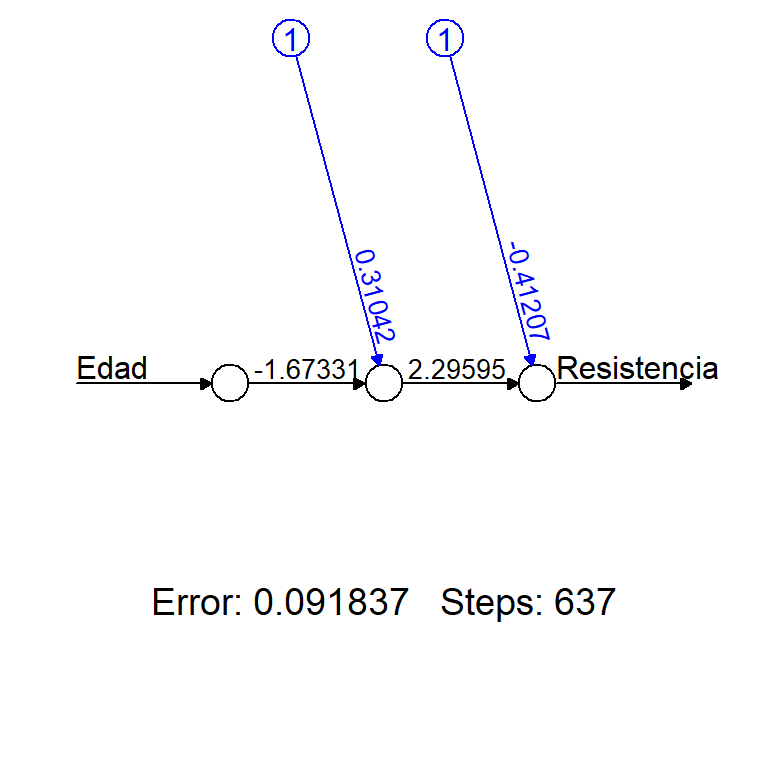
                  hidden=c(1), threshold=0.01)

Se puede construir un dibujo con la red ajustada usando la función plot sobre el objeto mod1.

plot(mod1, rep="best")

El objeto mod1 tiene varios elementos en su interior, para ver lo que hay dentro podemos usar el código siguiente.

names(mod1)

##  [1] "call"                "response"            "covariate"          
##  [4] "model.list"          "err.fct"             "act.fct"            
##  [7] "linear.output"       "data"                "exclude"            
## [10] "net.result"          "weights"             "generalized.weights"
## [13] "startweights"        "result.matrix"

El elemento act.fct es la función de activación (logística por defecto) y el elemento weights contiene los pesos mostrados en la anterior figura. Estos dos elementos serán útiles más adelante. A continuación el código para explorar lo que hay dentro de estos dos elementos.

mod1$act.fct          # Activation function

## function (x) 
## {
##     1/(1 + exp(-x))
## }
## <bytecode: 0x0000000017e931b0>
## <environment: 0x0000000017e91d20>
## attr(,"type")
## [1] "logistic"

unlist(mod1$weights)  # To obtain weights in vector form

## [1]  0.3104208 -1.6733110 -0.4120695  2.2959502

Predicción

En este ejemplo la base de datos tiene solo 20 observaciones y por esta razón el conjunto de entrenamiento y conjunto de prueba son el mismo.

En el código mostrado a continuación se crea el conjunto de prueba test solo con la covariable Edad proveniente de la base scaled. La función compute permite predecir los valores Resistencia para la informacion disponible en test teniendo como referencia una red neuronal entrenada, en este caso vamos a usar mod1.

test <- data.frame(Edad = scaled$Edad)
myprediction <- compute(x=mod1, covariate=test)

El objeto myprediction tiene varios elementos y uno de ellos es $net.result que contiene las predicciones. A continuación vamos a explorar los 5 primeros valores.

myprediction$net.result[1:5]

## [1] 0.36420817 0.09056855 0.66362440 0.30916344 0.76791814

Una pregunta que el lector debe tener en este momento es ¿de dónde vienen los valores anteriores?

Para responder la pregunta vamos a tomar como ejemplo el primer valor de la Edad escalada, es decir el valor 0.5869565, y con ella vamos a estimar el valor de resistencia escalada. Vamos introducir este valor en la red número uno y vamos a realizar las operaciones indicadas en la figura asociadas a mod1.

$\begin{aligned} {\hat{R e s i s t e n c i a}}_{1} & = F u n A c t (E d a d_{1} \times - 1.673311 + 0.3104208) \times 2.2959502 + - 0.4120695 \\ = F u n A c t (0.5869565 \times - 1.673311 + 0.3104208) \times 2.2959502 + - 0.4120695 \\ = 0.3642082 \end{aligned}$

Del anterior resultado vemos que ${\hat{R e s i s t e n c i a}}_{1}$ coincide con el valor obtenido de myprediction$net.result[1], esto responde las dos preguntas anteriores.

Otro aspecto importante es que el elemento $net.result del objeto myprediction tiene el $\hat{y}$ o respuesta estimada pero en la forma escalada, por esta razón es necesario aplicar la transformación inversa para obtener el resultado en la escala original. A continuación el código necesario para retornar a la escala original.

yhat_red <- myprediction$net.result * (max(datos$Resistencia)-min(datos$Resistencia))+min(datos$Resistencia)
datos$yhat_red <- yhat_red
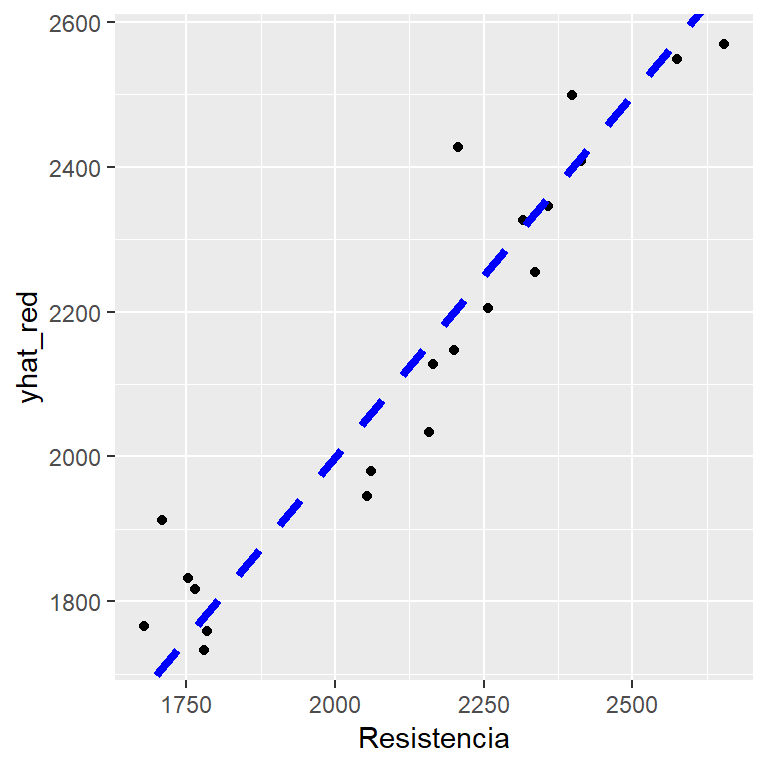
yhat_red[1:5] # Para ver los primeros 5 valores estimados

## [1] 2033.635 1766.549 2325.881 1979.909 2427.677

Para comparar los resultados obtenidos con la red neuronal podemos dibujar los valores observados $y$ contra los valores $\hat{y}$ . A continuación se muestra el código para crear el gráfico de dispersión al cual se le agrega un línea recta a 45 grados como referencia; entre más cerca este un punto de la línea, significa que $\hat{y}$ y $y$ son cercanos.

ggplot(datos, aes(x=Resistencia, y=yhat_red)) + geom_point() +
  geom_abline(intercept=0, slope=1, color="blue", linetype="dashed", size=1.5)

Del gráfico anterior podemos ver que las estimaciones $\hat{y}$ son cercanas a los verdaderos $y$ , adicionalmente el coeficiente de correlación lineal calculado es de 0.9469494 lo cual es un valor alto.

Comparación con un modelo lineal simple

Montgomery, Peck and Vining (2003) en el ejemplo 2.1 ajustaron un modelo de regresión lineal simple el cual se puede replicar con el siguiente código.

mod2 <- lm(Resistencia ~ Edad, data=datos)
coef(mod2)

## (Intercept)        Edad 
##  2627.82236   -37.15359

Usando los resultados anteriores el modelo de regresión lineal simple sería

${\hat{R e s i s t e n c i a}}_{i} = 2627.82236 - 37.15359 \times E d a d_{i}$

Los valores estimados para la resistencia con el modelo lineal simple se pueden obtener de la siguiente manera.

yhat_mls <- fitted(mod2)
yhat_mls[1:5] # Para ver los primeros 5 valores estimados

##        1        2        3        4        5 
## 2051.942 1745.425 2330.594 1996.211 2423.478

Para comparar la red neuronal con el modelo lineal simple vamos a usar el $E C M$ dado por la siguiente expresión:

$E C M = \frac{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}{n}$

ecm_red <- mean((datos$Resistencia - yhat_red)^2)
ecm_red

## [1] 8749.106

ecm_rls <- mean((datos$Resistencia - yhat_mls)^2)
ecm_rls

## [1] 8312.743

Red neuronal con dos capas

Como ilustración vamos a construir una segunda red con dos capas, la primera con 2 nodos y la segunda con 3 nodos, a continuación el código.

mod3 <- neuralnet(Resistencia ~ Edad, data=scaled, 
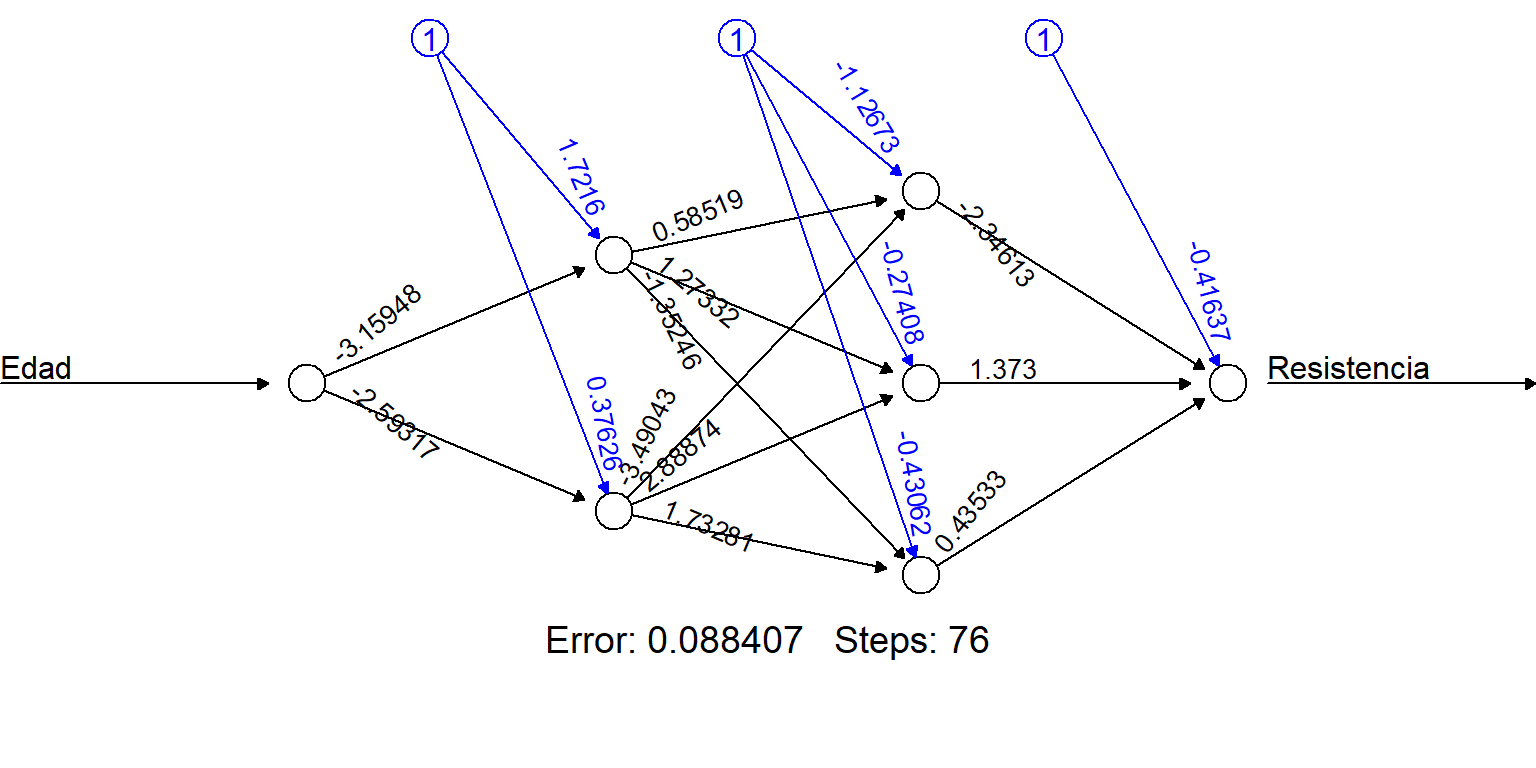
                  hidden=c(2, 3), threshold=0.01)

Nuevamente podemos dibujar la red construída.

plot(mod3, rep="best")

Redes neuronales con neuralnet

Freddy Hernández

2019/05/28

Introducción

Los datos

Paquete `neuralnet`

Creando la red neuronal

Predicción

Comparación con un modelo lineal simple

Red neuronal con dos capas

Redes neuronales con neuralnet

Freddy Hernández

2019/05/28

Introducción

Los datos

Paquete neuralnet

Creando la red neuronal

Predicción

Comparación con un modelo lineal simple

Red neuronal con dos capas

Paquete `neuralnet`